האליפסה

האליפסה מוגדרת כאוסף של נקודות (מקום גיאומטרי של נקודות)
אשר סכום מרחקיהן משתי נקודות קבועות (הנקראות מוקדים), הוא סכום קבוע.
בואו ונראה למה הכוונה:

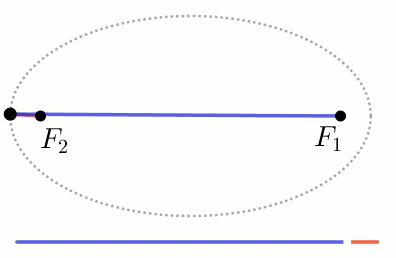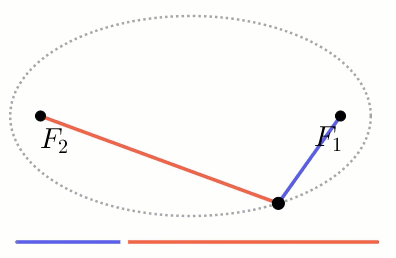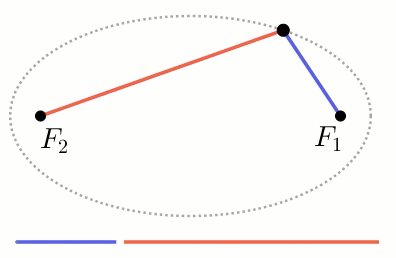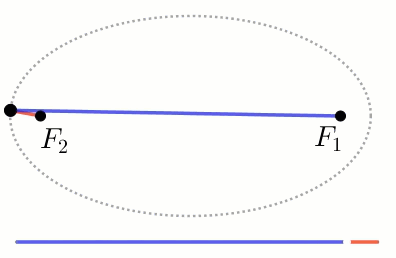
אם נציב את אותם המוקדים באופן סימטרי על ציר ה X או על ציר ה Y
נקבל את האליפסה הקנונית ביחס למערכת הצירים.

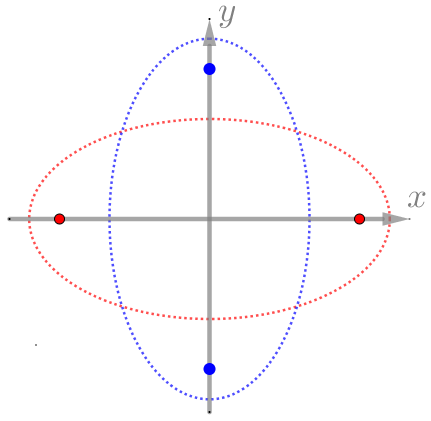
כדי לבנות את משוואת האליפסה נסמן את הפרמטרים הבאים:
את נקודות המוקד נסמן

F_1(C,0) \ \ , \ \ F_2(-C,0)

את נקודות החיתוך של האליפסה עם ציר ה X נסמן

(a,0) \ \ , \ \ (-a,0)

את נקודות החיתוך של האליפסה עם ציר ה Y נסמן

(0,b) \ \ , \ \ (0,-b)

למרחקי כל נקודה שעל האליפסה עם המוקדים נקרא רדיוס ווקטור ונסמן

r_1\ \ , \ \ r_2

כך שמתקיים 

r_1+ r_2=2a

ואז משוואת האליפסה הקנונית תוצג באחת משתי האפשרויות הבאות

\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ \ , \ \ b^2x^2+a^2y^2=a^2b^2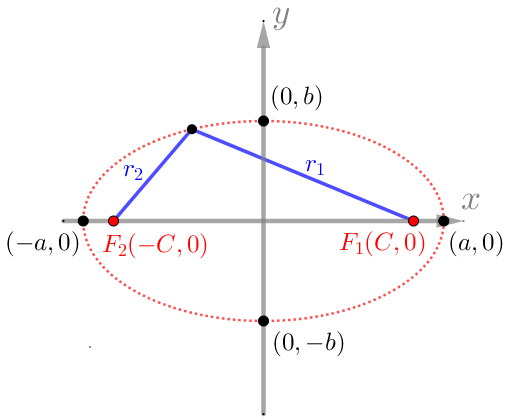

מידע נוסף , משפטים תרגילים ודוגמאות , אפשר לקבל בסרטים הבאים